Τόξα

«Σε επιστημονικές ερωτήσεις, η εξουσία χιλίων ανθρώπων δεν αξίζει όσο η ταπεινή λογική του ενός.»

Γαλιλαίος

Η στατική καθαρότητα βασικών γεωμετρικών μορφών θα είναι από τις κύριες παραμέτρους αυτής της καινούργιας στήλης. Η καταφυγή σε απλές γεωμετρίες είναι απαραίτητη, εάν κάποιος έχει σκοπό αρχικά να κατανοήσει θεμελιώδεις αρχές και αργότερα να συνθέσει πάνω σε αυτές. Ιστορικά, κάθε σημαντική καινοτομία στον χώρο της μηχανικής και της αρχιτεκτονικής συνέβη ταυτόχρονα με απλούστευση των προβλημάτων και με αμφισβητήσεις και έρευνα πολύ αρχικών μορφών.
Μία από τις πιο βασικές γεωμετρίες και από τις πιο επαναστατικές και όμορφες ανακαλύψεις στην μηχανική, με ατελείωτες αρχιτεκτονικές εφαρμογές είναι αναμφισβήτητα το τόξο. Η στατική ευκρίνεια που μεταφράζεται σαν ιδιαίτερη ικανότητα στην παραλαβή των φορτίων καθώς και η αισθητική επάρκεια, είναι χαρακτηριστικά που κάνουν τόξα όπου και να εμφανίζονται, να ξεχωρίζουν και να εντυπωσιάζουν ακόμη και σήμερα.

Πανέμορφο τοξωτό γεφύρι πάνω από τον ποταμό Αώο
(φωτογραφία από το konitsa.gr)

Αρχικά, είναι σίγουρα απαραίτητο να παρουσιαστεί και να ξεκαθαριστεί η στατική λειτουργία του τόξου. Πως λειτουργεί ένα τόξο; Είναι μόνο η αρχιτεκτονική του κομψότητα και το εμβληματικό του εκτόπισμα που παρακινεί μηχανικούς και αρχιτέκτονες να το χρησιμοποιούν τόσο συχνά;
Η απάντηση όπως και σε όλα τα αντίστοιχα ερωτήματα δεν μπορεί να είναι μονοσήμαντη. Σίγουρα η ομορφιά και η ελκυστικότητα ενός τόξου οδηγεί στο να διαλέγεται τόσο πολύ από τους σχεδιαστές, είναι όμως και ένας άλλος λόγος, αν όχι παραπάνω, τουλάχιστον εξίσου σημαντικός. Και αυτός είναι, ότι το κυριότερο πλεονέκτημα των τοξοτών κατασκευών είναι η ιδιότητα τους να παραλαμβάνουν τα επιβαλλόμενα φορτία, μεταφράζοντάς τα σχεδόν αποκλειστικά σε αξονικές δυνάμεις.
Όταν άρχισε το τόξο να χρησιμοποιείται για πρώτη φορά , πολλά από τα υλικά της εποχής δεν είχαν την δυνατότητα να παραλαμβάνουν σημαντικές εφελκυστικές τάσεις. Δεν υπήρχε η έννοια του οπλισμένου σκυροδέματος (ούτε καν η έννοια του σκυροδέματος), η δυνατότητα κατασκευής καλωδίων, η δυνατότητα παραγωγής χάλυβα ισχυρών ιδιοτήτων και όλων των υπολοίπων μέσων που χρησιμοποιούν οι μηχανικοί και οι αρχιτέκτονες σήμερα για να παραλάβουν μεγάλες εφελκυστικές τάσεις. Τέτοια εφόδια που σήμερα είναι καθημερινότητα, δεν υπήρχαν στην φαρέτρα τους. Η αδυναμία αυτή οδηγούσε το σύνολο των δημιουργών της εποχής στο σχεδιασμό βαριών φορέων, που δούλευαν κυρίως σε θλίψη και έτσι το τόξο ήταν η ιδανική γεωμετρία, μιας και δημιουργεί μόνο τέτοιες εντάσεις.

 Πανέμορφο τοξωτό γεφύρι πάνω από τον ποταμό Βοϊδομάτη
(φωτογραφία από το konitsa.gr)

Το πιο σημαντικό ερώτημα που γεννιέται αυτομάτως βέβαια είναι: έχει οποιαδήποτε τοξωτή γεωμετρία αυτό το χαρακτηριστικό? Ποια είναι η κατάλληλη εξίσωση που περιγράφει αυτή τη γεωμετρία? Όταν λέμε τόξο εννοούμε όντως τόξο κύκλου? Είναι μέρος παραβολής? Είναι κάποια άλλη συνάρτηση? Είναι μία συνάρτηση ή μεταβάλλεται κατά μήκος του?
Μην βιαστείτε να απαντήσετε… ακόμα και ο Γαλιλαίος σε αυτή την ερώτηση έκανε λάθος. Στην πραγματικότητα, η ιστορία περιγράφει ότι στην ερώτηση, «Ποια συνάρτηση δημιουργείται αν κρεμάσουμε μία αλυσίδα από τις δύο άκρες της;», ο Γαλιλαίος απαντούσε με σιγουριά: η παραβολή! Έπρεπε να έρθει ένας εκ των Bernoulli’s, περίπου 30 χρόνια μετά, για να ερευνήσει και να αποδείξει τελικά την πραγματική εξίσωση της κρεμάμενης αλυσίδας (ή αλλιώς catenary από το λατινικό catena, δηλαδή το σημερινό καδένα που όλοι χρησιμοποιούμε).

Η φυσική σημασία αυτού του φαινομενικά άσχετου ερωτήματος έμελλε να παίξει τεράστιο ρόλο στην μηχανική έκτοτε. Αποδείχτηκε ότι το τέλειο τόξο, το τόξο δηλαδή που εξαφανίζει οποιοδήποτε καμπτικό φαινόμενο υπό το ίδιο βάρος του, είναι αυτό που ακολουθεί την εξίσωση της κρεμάμενης αλυσίδας που ο Γαλιλαίος ήθελε ως παραβολή. Ας μην ξεχνάμε ότι την μέθοδο αυτή για να βρίσκει την βέλτιστη γεωμετρία χρησιμοποίησε κατά κόρον και ο Antonio Gaudi, μετά από 250 χρόνια, για να κατασκευάσει το πασίγνωστο Park Güell και φυσικά την πανέμορφη Sagrada Familia. Πολλά από τα τόξα μέσα στο Park Güell είναι προϊόντα αυτής της μεθόδου και ακολουθούν την εξίσωση της κρεμάμενης αλυσίδας. Ο τρόπος σχεδιασμού του Antonio Gaudi θα αναλυθεί λεπτομερώς σε επόμενο άρθρο αφού παρουσιάζει εξαιρετικό ενδιαφέρον.
Ποια είναι λοιπόν αυτή η μαθηματική σχέση; Πως προκύπτει το σχήμα που εξαφανίζει την κάμψη και παρουσιάζει μόνο αξονικές δυνάμεις; Σε καμία περίπτωση, σκοπός του παρόντος άρθρου δεν είναι να παρουσιάσει πολύπλοκες μαθηματικές εξισώσεις ή δυσνόητους υπολογισμούς, γι’ αυτό, παραθέτουμε αμέσως παρακάτω το αποτέλεσμα και αυτή την μνημειώδη εξίσωση:

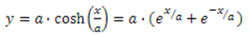
όπου α, ένας συντελεστής που εξαρτάται από το μήκος της αλυσίδας και κατ’ επέκταση από το ίδιο βάρος της κατασκευής (το υλικό δηλαδή). Είναι φανερό λοιπόν ότι η εξίσωση που αποτελεί την συνάρτηση που περιγράφει την γεωμετρία μιας αλυσίδας υπό καθαρό εφελκυσμό και ενός τόξου υπό καθαρή θλίψη είναι πολύ διαφορετική (μαθηματικά) και από την εξίσωση του κύκλου αλλά και από της παραβολής.

Το τόξο στο St. Louis, MO, USA

Προς επιβεβαίωση όλων των παραπάνω και για να αποδείξουμε και εμείς ότι Γαλιλαίος είχε όντως άδικο, κάναμε την παρακάτω άσκηση. Υποθέσαμε ότι έχουμε ένα άνοιγμα 80μ. που πρέπει να γεφυρωθεί με μία τοξωτή γέφυρα.
Ο μόνος περιορισμός, (μαθηματικός, ώστε να μπορούν να οριστούν οι συναρτήσεις και να αποφευχθούν πολλαπλές λύσεις), είναι το ύψος της γέφυρας από το έδαφος, που ορίζεται στα 15μ.

Στο παρακάτω σχήμα σχεδιάστηκαν τα τρία ενδεχόμενα. Σχεδιάστηκε ένα τόξο κύκλου, μία παραβολή και μία εξίσωση catenary. Το πρώτο γρήγορο και ταυτόχρονα όχι και πολύ λανθασμένο συμπέρασμα είναι ότι οι τρεις συναρτήσεις δεν διαφέρουν και δραματικά και είναι αλήθεια ότι οι γεωμετρικές αποκλίσεις μεταξύ τους δεν είναι πολύ μεγάλες.

Τα τρία ενδεχόμενα σχεδιασμένα μαζί (κύκλος, παραβολή, catenary)

Μετά από την σχεδίαση των τριών συναρτήσεων, αρθρώσαμε τα άκρα τους στο έδαφος και κάναμε την πιο απλή και καθοριστική όμως ανάλυση. Αφού τρέξαμε τα τρία διαφορετικά μοντέλα σε ένα πρόγραμμα πεπερασμένων στοιχείων, βγάλαμε αποτελέσματα για την φορτιστική κατάσταση του ίδιου βάρους. Τα αποτελέσματα είναι εντυπωσιακά και παρουσιάζονται παραστατικά στο παρακάτω σχήμα.

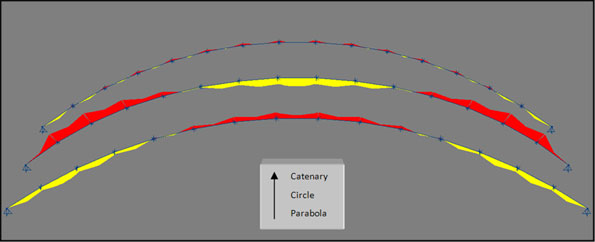
Αποτελέσματα ανάλυσης. Διάγραμμα ροπών για τα τρία ενδεχόμενα

Από κάτω προς τα πάνω τα τόξα είναι: η παραβολή, ο κύκλος και το catenary. Τα κόκκινα και κίτρινα είναι οι αρνητικές και θετικές ροπές αντίστοιχα σε κλίμακα. Είναι προφανές ότι στην παραβολή και τον κύκλο υπάρχει κάμψη και μάλιστα σημαντική, ενώ στο catenary η κάμψη είναι σχεδόν ανύπαρκτη.
Αποτέλεσμα αυτού του γεγονότος είναι ότι στο catenary δεν εμφανίζονται καθόλου εφελκυστικές τάσεις, έχουμε καθαρή θλίψη και άρα μόνο θλιπτικές τάσεις. Δηλαδή θα μπορούσαμε για την συγκεκριμένη γέφυρα να χρησιμοποιήσουμε μόνο πέτρα που έχει πολύ υψηλή αντοχή θλίψης αλλά πολύ χαμηλή αντοχή εφελκυσμού (λαμβάνοντας μόνο υπόψη το ίδιο βάρος).

Σίμος Γερασιμίδης
Υποψήφιος Διδακτορας,
Εργαστήριο Μεταλλικών Κατασκευών, Α.Π.Θ.

Αναφορές:
1. http://en.wikipedia.org/wiki/Catenary
2. http://whistleralley.com/hanging/hanging.htm
3. http://www.konitsa.gr
4. http://www.abbeville.com/excerpts.asp?ISBN=0789206900
5. http://architecture.mit.edu/people/bg/cvochsen.html